This is not really IT related, but geeky enough, I guess.
The other day I read a post or article about job interviews in the tech sector, like Google et al... And - so the article went - Google (if I recall correctly) once asked a candidate what his favorite (mathematical) equation was.
That made me think...
So here are my favorite equation(s) - not a surprising choice, given that my background is electrical engineering.
1. Euler's Equation (wikipedia link)
This one keeps fascinating me since I first heard it in an early math lecture at TechU Vienna. It goes like this
(or rather substitute a j for the i... as I said - electrical engineering :) )
What's so fascinating about it, you ask?
Well, it contains 5 elementary constants/numbers (0, 1, e, π, j) and it contains the 3 basic arithmetic operations (addition, multiplication, exponentiation)... more on Wikipedia.
2. Maxwell's Equations (Wikipedia link)
No surprise here for an electrical engineer, again, right ?
I'll show the most simple (and differential) form here, since I think this shows their beauty best:



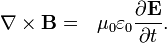 For an explanation and the more general form, check out Wikipedia.
For an explanation and the more general form, check out Wikipedia.
And why those?
Well I think the symmetry is apparent. And they are so fundamental to basically everything
Also, according to Wikipedia, I'm not really alone with that choice:
So... rather mainstream, right? Would not get me a job at Google :)
The other day I read a post or article about job interviews in the tech sector, like Google et al... And - so the article went - Google (if I recall correctly) once asked a candidate what his favorite (mathematical) equation was.
That made me think...
So here are my favorite equation(s) - not a surprising choice, given that my background is electrical engineering.
1. Euler's Equation (wikipedia link)
This one keeps fascinating me since I first heard it in an early math lecture at TechU Vienna. It goes like this
(or rather substitute a j for the i... as I said - electrical engineering :) )
What's so fascinating about it, you ask?
Well, it contains 5 elementary constants/numbers (0, 1, e, π, j) and it contains the 3 basic arithmetic operations (addition, multiplication, exponentiation)... more on Wikipedia.
2. Maxwell's Equations (Wikipedia link)
No surprise here for an electrical engineer, again, right ?
I'll show the most simple (and differential) form here, since I think this shows their beauty best:



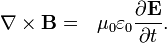
And why those?
Well I think the symmetry is apparent. And they are so fundamental to basically everything
Also, according to Wikipedia, I'm not really alone with that choice:
A poll of readers conducted by The Mathematical Intelligencer magazine named Euler's Identity as the "most beautiful theorem in mathematics". Another poll of readers that was conducted by Physics World magazine, in 2004, chose Euler's Identity tied with Maxwell's equations (of electromagnetism) as the "greatest equation ever".
So... rather mainstream, right? Would not get me a job at Google :)

No comments:
Post a Comment